. Figure 5 describes our new parametric form of a circle.
Robert is a senior software engineer for International Laser Machines and can be reached at 4645 Orlando Ct., Indianapolis, IN 46208.
As graphical PCs become increasingly popular, end-users continue to demand faster response rates until their problem can be modeled interactively in real time. The obvious solution to the problem of minimizing calculation and regeneration time is faster hardware, but this is the brute force solution. Let's instead look at producing better software through clever algorithms. This solution can produce time savings that are an order of magnitude faster. This article describes an algorithm for efficient circle generation and shows how this is achievable through a modest amount of mental gymnastics.
In computer graphics, circle (and ellipse) generation is an operation as fundamental as line drawing and point plotting. The obvious approach to generating the (Xk, Yk) pairs needed to describe the circumference of the circle is shown in the equation in Figure 1. However, this implicit nonparametric representation of the circle has three problems.
First, a circle has multiple Y values for a given X value. This necessitates solving the equation in Figure 1 for Ykto produce the equation in Figure 2. Because the goal is to produce a fast algorithm, it is best to avoid the extraction of the roots. The second problem deals primarily with the aesthetics of the curve. When the Xks are evenly spaced, the results are poor due to the uneven distribution of points along the length of the curve in Figure 3.
Finally, implicit nonparametric curves are axis-dependent. The implication here is that the choice of coordinate systems can affect the ease of calculation. This becomes especially apparent when the end point of a curve has a vertical slope relative to the chosen coordinate system. These problems are why we will switch to parametric representations.
The parametric form of each point on the circumference of the circle can be represented as two functions of one variable. There are many possible choices for the functions and parameters. The equation representing Figure 3 can be converted to its normalized parametric equivalent according to the equation in Figure 4. However, as previously mentioned, Figure 3 was an example of a computationally inefficient and aesthetically displeasing portion of a circle. This leads us to search for a different parameter. As such, we will look to polar representations with the parameter . Figure 5 describes our new parametric form of a circle.
At first glance, Figure 5 might not seem like much of an improvement over the equation in Figure 2 or Figure 4. The evaluation of the sine and cosine functions can be just as costly from a computational standpoint as the extraction of the square root. We could precompute a table of sine values, but this would limit us to a fixed number of points. The way to calculate the (Xk, Yk)pairs is by rearranging the equation in Figure 5. Observe that ks used in Figure 5 can be generated from the previous value via the relation k+1 = k +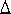 
s. If we take the cosine of both sides of the previous equation, we have cos(sk+1) = cos(sk + 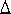s). The right side of this equation can be expanded by using the trigonometric identity for the cosine of an angle s and some 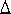s. The identity is shown in Figure 6.
If you now multiply by R, the radius of the circle, you will essentially have the equation in Figure 5. However, because the right side has been expanded, according to the equation in Figure 6, what you will actually be left with is the equation in Figure 7. The significance of this expansion can be found in the third line of the equation for both Xk+1 and Yk+1. The use of the trig identity shows that Xk+1 is partially described in terms of Xk and Yk, leaving us with a recurrence relation. Notice that the Xk and Yk values are multiplied by the sine and cosine of 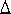s, a numeric constant! The implication of these algebraic gyrations is that the calculation of the equation in Figure 7 is simply the sum of the product of two sets of numbers.
Please note that Figure 7 will generate the points on the circumference of a circle centered at the origin. In general, if the circle is centered at the point (a,b), then the equation in Figure 8 will be of greater interest.
My answer to the problem of circle generation begins with the obvious mathematical solution. From there, creative exploration of the solution space starts with trigonometric representations that are not well-suited for computers. However, the application of an identity leaves us with a solution using operations that are an intrinsic part of any computational unit. I've taken this as far as I can go and look forward to your improvements.